让不懂建站的用户快速建站，让会建站的提高建站效率！
发布日期：2024-11-04 16:12 点击次数：117
若D为线段BC的中点，A为恣意少量，则有：2AD²+BC²/2=AB²+AC²。
若A点不在BC上，如下图，即为三角形中线定理。
这里不再说明，有兴趣的不错查阅辛苦。
若A点在BC上，假定A在BD之间，如下图。
2AD²+BC²/2=2AD²+2BD²，而AB²+AC²=(BD+AD²)+(BD-AD)²=2BD²+2AD²，是以有2AD²+BC²/2=AB²+AC²。
至极的，当A点与B点重合时，原式变为2BD²+BC²/2=BC²，当A点与D点重合时，原式变为BC²/2=BD²+DC²。
固然，若A点在DC之间，可得出相通论断，不再赘述。
底下这说念题用到了中线定理。如下图，ABCD为空间四点，求证：
AC²+AD²+BC²+BD²≥AB²+CD²。
365站群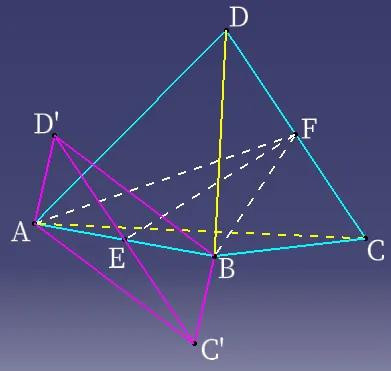
说明：取AB、CD中点E、F，流通AE、BE、EF。
在△ACD中，AC²+AD²=2AF²+CD²/2
365建站客服QQ：800083652在△BCD中，BC²+BD²=2BF²+CD²/2
是以AC²+AD²+BC²+BD²=2AF²+2BF²+CD²又在△ABF中，AF²+BF²=2EF²+AB²/2，AC²+AD²+BC²+BD²≥4EF²+AB²+CD²≥AB²+CD²。
当EF重合时，如上图，CD变为C'D'，等号树立，此时AC'BD'变为平行四边形。